Discussion Forum



1)

For the first order reaction $2N_{2}O_{5}(g) \rightarrow  4NO_{2}(g)+O_{2} (g)$


A) the concentration of the reaciant decreases exponentially with time

B) the half-life of the reaction decreases with increasing temperature

C) the half-life of the reaction depends on the initial concentration of the reactant

D) the reaction proceeds of 99.57% completion in eight half-life duration

Answer:

Option A,B,D

Explanation:

(a) For a first-order reaction. the concentration of reactant remaining after time t is given by $[A]=[A]_{0}e^{-kt}$. Therefore, the concentration of  reactant decreases exponentially  with time 

8122021519_d4.PNG

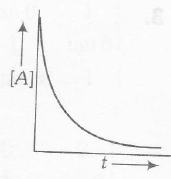
(b)   Rise in temperature  increase rate constant (k)  and  therefore decrease half-life $(t_{1/2})$ as

                           $t_{1/2}=\frac{ln 2}{k}$

 (d) For a first order reaction. if 100 moles of reactant is taken  initially, after  n half-lives reactant remaining is given by percentage

  $A= 100(\frac{1}{2})^{n}=100(\frac{1}{2})^{8}=0.3906$

$\Rightarrow $  A  reacted =100-0.3906=99.6%

(c) Half-life of first order reaction is independent of initial concentration