Discussion Forum

The straight line 2x - 3y = 1 divides the circular region $x^{2}+y^{2}\leq 6$ into two  parts  .If  $S=\left\{\left(2,\frac{3}{4}\right),\left(\frac{5}{2},\frac{3}{4}\right),\left(\frac{1}{4},-\frac{1}{4}\right),\left(\frac{1}{8},\frac{1}{4}\right)\right\}$, then the  number of point(s) in S lying inside the smaller part is 

Answer:

Explanation:

$x^{2}+y^{2} \leq 6$  and 2x-3y=1 is shown as,

For the point to lie in the shaded part, origin and the point lie on opposite side
of straight line L.

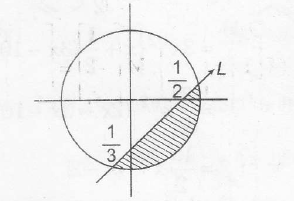
 $\therefore$ For any point in shaded part L >0

 and for any point inside the circle S <0

 Now, for $\left(2,\frac{3}{4}\right) L:2x-3y-1$

 $L:4-\frac{9}{4}-1 =\frac{3}{4} >0$

 and   $S:x^{2}+y^{2}-6,$

 $S:4+ \frac{9}{16} -6<0$

 $\Rightarrow$   $\left(2,\frac{3}{4}\right)$  lies in shaded part

 For  $\left(\frac{5}{2},\frac{3}{4}\right)L:5-9-1<0$ {neglect}

 For $\left(\frac{1}{4},-\frac{1}{4}\right)L:\frac{1}{2}+\frac{3}{4}-1>0$ }

 $\therefore$ $\left(\frac{1}{4},-\frac{1}{4}\right)$  lies in the shaded part

 For $\left(\frac{1}{8},\frac{1}{4}\right)$L:$\frac{1}{4}-\frac{3}{4}-1 <0$ [neglect]

 $\Rightarrow$   only 2  points lie in the shaded  part