Answer:
Option D
Explanation:
(P) Plan
(i) For such questions , we need to properly define the functions and then we draw their graphs.
(ii) From the graphs,we can examine the function for continuity differentiability , one-one and onto
$f_{1}(x)=\begin{cases}-x & x < 0\\e^{x} & x \geq 0\end{cases}$
$f_{2}(x)=x^{2},x\geq0$
$f_{3}(x)=\begin{cases}sin x & x < 0\\x & x \geq 0\end{cases}$
$f_{4}(x)=\begin{cases}f_{2}(f_{1}(x)) & x < 0\\f_{2}(f_{1}(x)) -1 & x \geq 0\end{cases}$
Now, $f_{2}(f_{1}(x)=\begin{cases} x^{2},& x < 0\\e^{2x}, & x \geq 0\end{cases}$
$f_{4}=\begin{cases} x^{2},& x < 0\\e^{2x}-1, & x \geq 0\end{cases}$
As f4(x) is contiinuous
$f'_{4}=\begin{cases} 2x,& x < 0\\2e^{2x}, & x > 0\end{cases}$
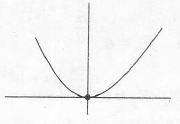
$f'_{4}(0)$ is not defined
Its range is [0, $\infty$]
Thus, range= codomain =[0,$\infty$] thus f4 is onto.
Also, horizontal line (drawn parallel to x-axis) meets the curve more than once function is not one-one
(Q) Plan $f_{3}(x)$
differentiable at x=0 and not one-one
As evident, from the graph it is continuous and no sharp turn at X=0 , thus f(x) is differentiable at x=0
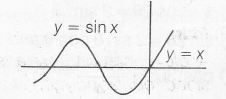
Also, a horizontal line intersects the graph more than once.
$\therefore$ It is not one-one
(R) Plan $f_{2}(f_{1}(x))$
It is neither continuous nor one-one.
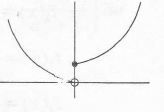
From the graph , it can be observed that the function is not continuous at x=0
Also , the horizontal line intersect,the curve at more than one point So, $f_{2}(f_{1}(x))$ , is not one-one
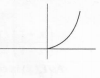
(S) f2(x)
It is continuous and one-one
As evident from graphs , the function is continuous
also, the function is one-one , as any horizontal line will meet the graph only one
$P\rightarrow(i), Q\rightarrow(iii),R\rightarrow(ii),S\rightarrow(iv)$