Discussion Forum

Two beams, A and B , of plane  polarised light with mutually perpendicular planes of polarisation are seen through a polarised. From the position  when the beam  A has  maximum intensity (and beam B has  zero intensity)  , a rotation of polarised through 30° makes the two beams appear equally bright. If the initial intensities  of the  two beams are I_A and I_B  respectively, then I_A/I_B equals

Answer:

Explanation:

By law of Malus  i.e,   $I=I_{0}\cos^{2}\theta$

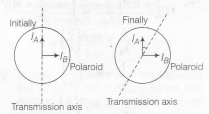
Now,   $I_{A'}=I_{A}\cos^{2}30^{0}$

            $I_{B'}=I_{B}\cos^{2}60^{0}$

As,           $I_{A'}=I_{B'}$

           $I_{A}\cos^{2}30^{0}$=  $I_{B}\cos^{2}60^{0}$

     $\Rightarrow$          $I_{A} \frac{3}{4}=I_{B}\frac{1}{4}$

$\Rightarrow$       $\frac{I_{A}}{I_{B}}=\frac{1}{3}$