Discussion Forum



1)

Monochromatic light is incident on a glass prism of angle A. If the refractive index of the  material of the prism is μ, a ray incident at an angle θ, on the face AB would get  transmitted through the face AC of the prism provided

2622021521_m39.JPG


A) $\theta > \sin^{-1}\left[\mu\sin\left(A-\sin^{-1}\left(\frac{1}{\mu}\right)\right)\right]$

B) $\theta < \sin^{-1}\left[\mu\sin\left(A-\sin^{-1}\left(\frac{1}{\mu}\right)\right)\right]$

C) $\theta > \cos^{-1}\left[\mu\sin\left(A+\sin^{-1}\left(\frac{1}{\mu}\right)\right)\right]$

D) $\theta < \cos^{-1}\left[\mu\sin\left(A+\sin^{-1}\left(\frac{1}{\mu}\right)\right)\right]$

Answer:

Option A

Explanation:

 Central Idea:     The ray will get   transmitted through face AC if   $i_{AC}<i_{C}$  . Consider the ray diagram  is shown below

2622021266_m40.JPG

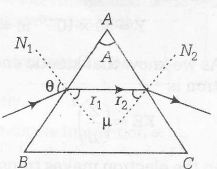
A ray of light incident on face AB at an angle θ

  $r_{1}$  = Angle of refraction on face AB

   $r_{2}$  = Angle of incidence at face AC

For transmission of light through face AC

  $i_{AC}<i_{C}$    or     $A-r_{1}<i_{C}$

 or             $\sin (A-r_{1})<\sin i_{C}$

or              $\sin (A-r_{1})<\frac{1}{\mu}$

                $A-r_{1}<\sin ^{-1}\left(\frac{1}{\mu}\right)$

       or             $\sin r_{1}>\sin \left[A-\sin ^{-1}\left(\frac{1}{\mu}\right)\right]$

 Now, applying snell's law at the face AB

   $1\times \sin \theta=\mu \sin r_{1}$    or  $ \sin r_{1}=\frac{\sin \theta}{\mu}$

  $\Rightarrow \frac{\sin \theta}{\mu}>\sin \left[A-\sin ^{-1}\left( \frac{1}{\mu}\right)\right]$

   or                      $\theta >\sin ^{-1}\left[\mu \sin\left\{A-\sin ^{-1}\left(\frac{1}{\mu}\right)\right\}\right]$