Answer:
Option D
Explanation:
Given the equation of curve is $x^{2}+2xy-3y^{2}=0 $ .......(i)
On differentiating w.r.t x, we get
$2x+2xy'+2y-6yy'=0$
$\Rightarrow$ $y'=\frac{x+y}{3y-x}$
At x=1, y=1, $y'=1$
i.e, $\left(\frac{\text{d}y}{\text{d}x}\right)_{(1,1)}=1$
Equation of normal at (1,1)
$y-1=-\frac{1}{1}(x-1)$
$\Rightarrow$ y-1=-(x-1)
$\Rightarrow$ x+y=2 ......(ii)
On solving Eqs .(i) and (ii) simultaneously , we get
$x^{2}+2x(2-x)-3(2-x)^{2}=0$
$\Rightarrow$ $x^{2}+4x-2x^{2}-3(4+x^{2}-4x)=0$
$\Rightarrow$ $-x^{2}+4x-12-3x^{2}+12x=0$
$\Rightarrow$ $-4x^{2}+16x-12=0$
$\Rightarrow$ $4x^{2}-16x+12=0$
$\Rightarrow$ $x^{2}-4x+3=0$
$\Rightarrow$ (x-1) (x-3)
$\Rightarrow$ x=1,3
Now, whern x=1 , then y=1
and when x=3, then y=-1
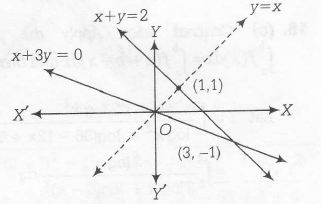
P =(1,1) and Q =(3,-1)
Hence, normal meets the curve again at (3,-1) in fourth quadrant.
Alter:
Given, $x^{2}+2xy-3y^{2}=0 $
$\Rightarrow$ (x-y)(x+3y)=0
$\Rightarrow$ x-y=0 or x+3y=0
Equation of normal at (1,1) is
y-1=-1(x-1)
$\Rightarrow$ x+y-2=0
It intersects x+3y=0 at (3,-1)
and hence normal meet the curve in fourth quadrant.