Discussion Forum

Let RS be the diameter of the circle  $x^{2}+y^{2}=1$, where S is the point (1,0). Let P be a variable point (other than R and S) on the circle and tangents to be a circle at S and P meet at the point Q. The normal to the circle at P.intersects  a  line drawn through Q parallel to RS at point  E.  Then, the locus of E passes through the point (s)

Answer:

Explanation:

Given, RS is the diameter of  $x^{2}+y^{2}=1$,

Here , equation of the tangent at   $P(\cos\theta,\sin\theta)$  is   $x\cos\theta+y\sin\theta=1$

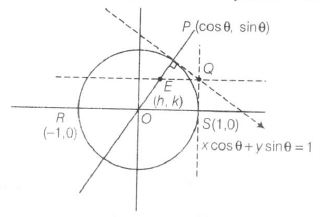
Intersecting with x=1

$y=\frac{1-\cos\theta}{\sin \theta}$

 $\therefore$     $Q\left(1.\frac{1-\cos\theta}{\sin\theta}\right)$

$\therefore$  Equation of the line through Q parallel to RS is

 $y=\frac{1-\cos \theta}{\sin\theta}=\frac{2\sin^{2}\frac{\theta}{2}}{2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}=\tan\frac{\theta}{2}$                      ............( i)

Normal at   $P:y=\frac{\sin\theta}{\cos\theta}.x$

 $\Rightarrow$   $y=x\tan\theta$                 ...........(ii)

Let their point of intersection be (h,k),

Then,    $k=\tan\frac{\theta}{2}$  and  $k=h\tan\theta$

$\therefore$   $k=h\left(\frac{2\tan\frac{\theta}{2}}{1-\tan^{2}\frac{\theta}{2}}\right)$

$\Rightarrow$    $k=\frac{2h.k}{1-k^{2}}$

$\Rightarrow$   $k(1-k^{2})=2hk$

 $\therefore$ Locus  for point  $E:2x=(1-y^{2})$   .....(iii)

when  $x=\frac{1}{3}$

then    $1-y^{2}=\frac{2}{3}$

$\Rightarrow$             $y^{2}=1-\frac{2}{3}$

$\Rightarrow$       $y=\pm\frac{1}{\sqrt{3}}$

$\therefore \left(\frac{1}{3},\pm\frac{1}{\sqrt{3}}\right)$   satisfy $2x=1-y^{2}$

when  $x=\frac{1}{4},$  then

$1-y^{2}=\frac{2}{4}$

$\Rightarrow$         $y^{2}=1-\frac{1}{2}$

$\Rightarrow$             $y=\pm\frac{1}{\sqrt{2}}$

$\therefore\left(\frac{1}{4},\pm\frac{1}{2}\right)$   does not satisfy  $1-y^{2}=2x$