Discussion Forum



1)

An infinitely long thin non-conducting wire is parallel to the Z-axis and carries a uniform line charge density λ . It pierces a thin non-conducting spherical shell of radius R in such a way that the arc PQ  subtends an angle 120° at the centre O  of  the spherical shell, as shown in the figure. The permittivity of free space is ε0 . Which of the following statements is (are) true?

109201912_circlr.JPG

 


A) The electric flux through the shell is $\sqrt{3}R\lambda /\epsilon_{0}$

B) The z-component of the electric field is zero at all the points on the surface of the shell.

C) The electric flux through the shell is $\sqrt{2}R\lambda /\epsilon_{0}$

D) The electric field is normal to the surface of the shell at all points.

Answer:

Option A,B

Explanation:

PQ= (2) R sin 60°

109201912_circlr.JPG

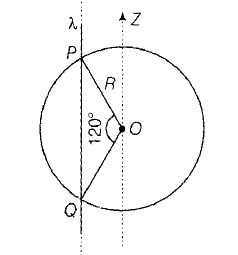
             = $(2R)\frac{\sqrt{3}}{2}=(\sqrt{3}R)$

             $q_{enclosed}=\lambda(\sqrt{3}R)$

 We have,        $\phi =\frac{q_{enclosed}}{\epsilon_{0}}$

$\Rightarrow$               $\phi =(\frac{\sqrt{3}\lambda R_{}}{\epsilon_{0}})$

Also,   electric field is perpendicular to wire, so Z- component will be zero.