Discussion Forum

 A small block starts sliding down an inclined plane forming an angle $45^{0}$ horizontal. The coefficient of friction $\mu$ varies with distance s as  $\mu=cs^{2}$ , where c is a constant of appropriate dimensions, then distance covered by the block before it stops is 

Answer:

Explanation:

Given that

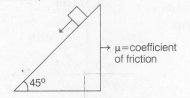
 $\mu= Cs^{2}$      [ $\because$ s= distance and C = constant ]

 net force on the block is 

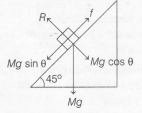
 $Mg\sin \theta- f=Ma$

$ Mg sin \theta - \mu  Mg \cos  \theta=Ma$

  $g \sin \theta- \mu g \cos \theta$=a

 $g[\sin \theta -Cs^{2} \cos \theta]=a$    ..........(i)

  $\because$        $a= \frac{dv}{dt}=v \frac{dv}{ds}$

 $ads=vdv$         ...........(ii)

 From eqs.(i) and (ii)  , we get

 $\Rightarrow$     $g[\sin \theta-Cs^{2} \cos \theta ]ds=vdv$

 Integreating  both sides , we get

 $\Rightarrow$     $(g\sin\theta)s-g\frac{Cs^{3}}{3}\cos\theta=\frac{v^{2}}{2}+K$  .....(iii)

 For  $\theta=45^{0}$, we have

$\left(\frac{g}{\sqrt{2}}\right)s-\left(\frac{Cs^{3}}{3}\right)\frac{g}{\sqrt{2}}=\frac{v^{2}}{2}+K$

Initially t=0, s=0 ,u=0 substitutingthese , we get k=0

 So,   $\frac{g}{\sqrt{2}}\left(s-\frac{Cs^{3}}{3}\right)=\frac{v^{2}}{2}$

$\Rightarrow  s-\frac{Cs^{3}}{3}=\frac{v^{2}}{2}\times \frac{\sqrt{2}}{g}$

 The body stops, when v=0  $\Rightarrow s-\frac{Cs^{3}}{3}=0$

 $\Rightarrow$     $s= \frac{Cs^{3}}{3}\Rightarrow s=\sqrt{\frac{3}{C}}$