Discussion Forum



1)

If a and b respectively represent the lengths of a side and a diagonal  of a regular pentagon that is inscribed in a circle , then $\frac{b}{a}$=


A) $2 \sin \frac{\pi}{5}$

B) $2 \cos \frac{\pi}{5}$

C) $ \cos \frac{\pi}{5}$

D) $\sin \frac{\pi}{5}$

Answer:

Option B

Explanation:

We have

a= side of pentagon

b= diagonal of regular pentagon

 1472021404_g1.PNG

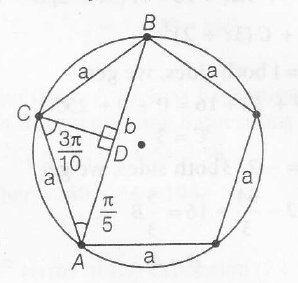
$\angle ACB= \frac{3 \pi}{5}$

$\angle ACD= \frac{3 \pi}{10} and \angle CAD=\frac{\pi}{5}$

 In $\triangle ACD$

   $\cos \frac{\pi}{5}=\frac{AD}{AC}\Rightarrow AD=a\cos \frac{\pi}{5}$

 $2AD=2a\cos \frac{\pi}{5}\Rightarrow \frac{b}{a}=$   $2 \cos \frac{\pi}{5}$