Online JEE 2016 Test ( Advanced 2016 )

A parallel beam of light is incident from the air at an angle $\alpha$ the side PQ of a right-angled triangular_prism of refractive index $n=\sqrt{2}$. Light undergoes total internal reflection in the prism at the face PR when $\alpha$ has a minimum value of 45⁰. The angle θ of the prism is

A uniform wooden stick of mass 1.6 kg of length / rests in an inclined manner on a smooth, vertical wall of height h (<l) such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of 30⁰  with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio  $\frac{h}{l}$ and the frictional force  f at the  bottom of the stick are (g = 10 ms^-2

A transparent slab of thickness d has a refractive index n (z)that increases with z. Here, z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n₁ and n₂ (> n₂ ) as shown in the figure. A ray of light is incident with angle θ_i , from medium 1 and emerges in medium 2 with refraction angle θ_f with a lateral displacement l.

Which of the following statement(s) is (are) true

Two inductors  L₁ (inductance lmH, internal resistance 3Ω) and k (inductance 2 mH, internal resistance 4 Ω), and a resistor R (resistance 12 Ω) are all connected in parallel across a 5V battery. The circuit is switched on at time t = 0. The ratio of the maximum to the minimum current (I_max , I_min ) drawn from the battery is

Consider two identical galvanometer and two identical resistors with resistance R. If the internal resistance  of the galvanometers

R_c < R/2, which of the following statement(s) about anyone is (are) true? 

A block with mass M is connected by a massless spring with stiffness constant k to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position x₀. Consider two cases : (i) when the block is at x₀  and (ii) when the block is at x=x₀ +A . In both the cases, a particle with mass m (<M)  is softly placed on the block after which they stick to each other. Which of the following statement(s) is (are) true about the motion after the mass m is placed on the mass M?

A frame of the reference that is accelerated with respect to an inertial frame of reference is called a non- inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of a non-inertial frame of reference. The relationship between the force $\overrightarrow{F}_{rot}$ experienced by a particle of mass m moving on the rotating disc and the force $\overrightarrow{F}_{in}$ experienced by the particle in an inertial frame of reference is,

$\overrightarrow{F}_{rot}= \overrightarrow{F_{in}}+2m(\overrightarrow{v}_{rot}\times\overrightarrow{\omega})+ m(\overrightarrow{\omega}\times \overrightarrow{r})\times\overrightarrow{\omega}$

where $V_{rot}$ is the velocity of the particle in the rotating frame of reference and r is the position vector of the particle with respect to center of the disc

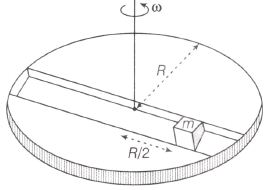
Now, consider a smooth slot along a diameter of a disc of radius R  rotating counter-clockwise with a constant angular speed ω about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and Z-axis along the rotation axis $(\omega =\omega\hat{k})$. A small block of mass m is gently placed in the slot at $r=(\frac{R}{2})\hat{i}$ at t=0 and is constrained to move only along the slot

The distance r of the block  at time t is

The geometries of the ammonia  complexes of Ni²⁺, Pt²⁺ and Zn²⁺ respectively are

Treatment of compound O with  $KMnO_{4}/H^{+}$ gave P, which on heating with ammonia gave Q. The compound Q on treatment with  $Br_{2}/NaOH$ produced R on strong heating, Q gave S which on further treatment with  ethyl 2-bromopropanoate in the presence of KOH followed by acidification gave a compound T

The compound T is

Area  of the region {(x,y)}ε $R^{2}:y\geq \sqrt{\mid x+3\mid},5y\leq (x+9)\leq15$ } is equal to

Let f:R→ (0,∞) and g: R→ R be twice differentiable functions such that f ’’ and g’’ are continuous functions on R

 Suppose  $f'(2)=g(2)=0, f''(2)\neq 0$ and $g'(2)\neq 0$, If  $\lim_{x \rightarrow 2}\frac{f(x)g(x)}{f'(x)g'(x)}=1$,  then

Let  $a,\lambda,\mu \epsilon R$ . Consider the system of linear equation ax+2y=λ and 3x-2y= μ . Which of the following statement(s) is (are ) correct?

Let  $F_{1}(x_{1},0)$ and $F_{2}(x_{2},0)$  , for  $x_{1}<0$ and $x_{2}>0$ , be the foci of the ellipise $\frac{x^{2}}{9}+\frac{y^{2}}{8}=1$ . Suppose a parabola  having vertex at the origin and focus at $F_{2}$ intersects the  ellipse  at the point M in the first quadrant and at point N  in the fourth quadrant

The orthocentre of  $\triangle F_{1}MN$ is 

Consider a pyramid OPQRS located in the first octant  $ (x\geq 0, y\geq 0,z\geq0)$ with O as origin, and OP and OR along the X-axis and the Y-axis, respectively. The base OPQR of the pyramid is a square with OP=3. The point S is directly above the mid-point T of diagonal OQ such that TS=3Then

Let $z=\frac{-1+\sqrt{3}i}{2}$ , where   $i=\sqrt{-1}$  , and  $ r,s \epsilon (1,2,3)$. Let  $P=\begin{bmatrix}(-z)^{r} & z^{2s} \\z^{2s} & z^{r} \end{bmatrix}$  and  I be the identity matrix of  order2.Then, the total number of ordered pairs (r,s) for which   $p^{2}=-I$ is