Definition:

A triangle is a 3 - sided polygon. If two sides of a triangle are equal, it is called isosceles triangle. If all the three sides are equal, it is called equilateral triangle. If all of the sides have different lengths, the triangle is scalene.

Classification of triangles by internal angles

1.Right triangle:

Right angle triangle has one of its interior angles measuring 90°. The side opposite to the right angle is called hypotenuse.

2. Acute triangle:

A triangle that has all interior angles measuring less than 90° isacute triangle.

3. Obtuse triangle :

A triangle that has one interior angle that measures more than 90° is an obtuse triangle

4. Degenerate:

A "triangle" with an interior angle of 180°

Properties of triangle :

1. The sum of the angles of a triangle is 180°.
2. The sum of the lengths of any two sides of the triangle is greater than the third side.
3. Pythagorean Theorem: The square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.

 

 

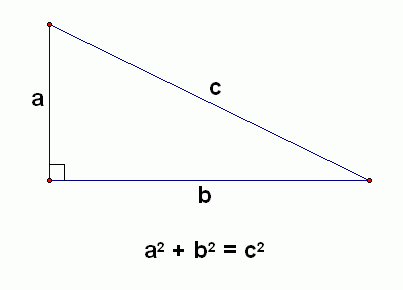
Differnt types

Similarity:

If two geometric figures are congruent they have the same shape and same size. Geometric figures which are of the same shape but not necessarily of the size are called similar figures.

Similar triangles :

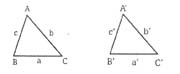
Two triangles, which have the three angles of one triangle equal to the three angles of the other triangle and all the ratios between the measures of corresponding sides equal are said to be similar.

If triangle ABC is similar to A' B' C then we write Δ ABC~ Δ A B' C

Note:
(i). Δ ABC is equiangular to Δ A' B' C,

then,

∠A = A'.∠B = ZB',∠C = ∠C

(ii) (a /a')= (b /b')  (  c/c') 

Important Results :

1. In a triangle, a line drawn parallel to one side to intersect the other sides in distinct points divides the two sides in the same ratio.
2. If a line divides any two sides of a triangle in the same ratio, then it is parallel to the third side.
3. The bisector of an angle of a triangle divides the opposite side in the ratio of the sides containing the angle.
4. If in two triangles, corresponding angles are equal (i.e) the two triangle are equiangular, then the triangles are similar.
5. If corresponding sides of two triangles are proportional, then they are similar.
6. If in two triangles one pair of corresponding sides are proportional and the included angles are equal, then the two triangles are similar.

Ratio of the areas of two similar triangles :

1. The ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
2. The areas of two similar triangles are in the ratio of the squares of the corresponding altitudes.
3. The areas of two similar triangles are in the ratio of the squares of the corresponding medians.
4. The areas of two similar triangles are in the ratio of the squares of the corresponding angle bisector segments.

Proportionality Theorem

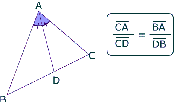
1. The bisector of an angle of a triangle divides the opposite side in the ratio of the sides containing the angle.
2. If the angle through one vertex of a triangle divides the opposite side in the ratio of the other two sides, then the line bisects the angle at the vertex.
3. If the bisector of the exterior ∠A of a ΔABC intersect the side

BC produced in D. Then, (AB/AC)=(BD/CD)

Numerrical Reasoning Questions