Answer:
Option D
Explanation:
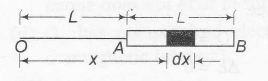
$V=\int_{L}^{2L} \frac{kdQ}{x}$
$=\int_{L}^{2L} \frac{k\left(\frac{Q}{L}\right)dx}{x}$
$=\frac{Q}{4 \pi \epsilon_{0}L}\int_{L}^{2L} \left(\frac{1}{x}\right)dx$
$=\frac{Q}{4 \pi \epsilon_{0}L}[\log_{e} x]_L^{2L}$
$=\frac{Q}{4 \pi \epsilon_{0}L}[\log_{e} 2L-\log_{e} L]$
$=\frac{Q}{4 \pi \epsilon_{0}L}ln(2)$