Answer:
Option A,B,C,D
Explanation:
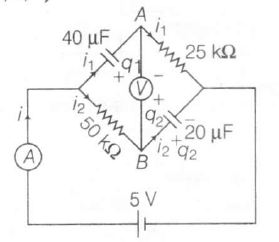
Just after pressing key,
5-25000i1 =0
5-50000 i2 =0
( As charge in both capacitors =0)
$\Rightarrow i_{1}=0.2mA\Rightarrow i_{2}=0.1mA$
And $V_{B}+25000i_{1}=V_{A}$
$\Rightarrow V_{B}-V_{A}=-5V$
After a long time , i1 and i2 =0 ( steady state)
$\Rightarrow 5-\frac{q_{1}}{40}=0\Rightarrow q_{1}=200\mu C$
and $ 5-\frac{q_{2}}{20}=0\Rightarrow q_{2}=100\mu C$
$V_{B}-\frac{q_{2}}{20}=V_{A}\Rightarrow V_{B}-V_{A}=+5 V$
$\Rightarrow$ (a) is correct.
For capacitor 1,
$q_{1}=200[1-e^{-\frac{t}{l}}]\mu C\Rightarrow i_{1}=\frac{1}{5}e^{-\frac{t}{l}}mA$
For capacitor 2,
$q_{2}=100[1-e^{-\frac{t}{l}}]\mu C\Rightarrow i_{2}=\frac{1}{10}e^{-\frac{t}{l}}mA$
$\Rightarrow V_{B}-\frac{q_{2}}{20}+i_{1}\times 25=V_{A}$
$\Rightarrow V_{B}-V_{A}=5[1-e^{-t}]-5e^{-t}$
$=-5[1-2e^{-t}]$
At t=ln 2,
$V_{B}-V=5[1-1]=0$
$\Rightarrow$ (b) is correct.
At t=1,
$i=i_{1}+i_{2}=\frac{1}{5}e^{-1}+\frac{1}{10}e^{-1}=\frac{3}{10}.\frac{1}{e}$
At t=0
$i=i_{1}+i_{2}=\frac{1}{5}+\frac{1}{10}=\frac{3}{10}$
$\Rightarrow$ (c) is correct
After a long time , $i_{1}=i_{2}=0$
$\Rightarrow$ (d) is correct.