Answer:
Option A
Explanation:
As E is constant
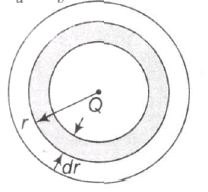
Hence , Ea ≡ Eb
A s per Guass theorem, only Q contributes in electric field
$\therefore \frac{kQ}{a^{2}}=\frac{k[Q+\int_{a}^{b}4\pi r^{2}dr.\frac{A}{r} }{b^{2}}$
Here, $k= \frac{1}{4\pi\epsilon_{0}}$
$\Rightarrow Q\frac{b^{2}}{a^{2}}=Q+4\pi A \left[\frac{r^{2}}{2}| _{a}^{b} \right]$
$=Q+4\pi A [\frac{b^{2}-a^{2}}{2}]$
$\Rightarrow Q (\frac{b^{2}}{a^{2}})=Q+2\pi A (b^{2}-a^{2})$
$\Rightarrow Q (\frac{b^{2}-a^{2}}{a^{2}})=2\pi A (b^{2}-a^{2})$
$\Rightarrow A= \frac{Q}{2\pi a^{2}}$